引言

　　在统计学中，主成分分析法（PCA）是一种可以将多维数据集转换为低维数据集的技术，以便更有效地进行可视化、分析和理解数据。随着数据科学和机器学习的不断发展，PCA已成为一种广泛使用的技术。本文以"2024精准资料免费大全"为主题，介绍轻量版8.53的主成分分析法，并提供详细的步骤和应用案例，旨在帮助研究人员和实践者更深入地理解和应用这一技术。

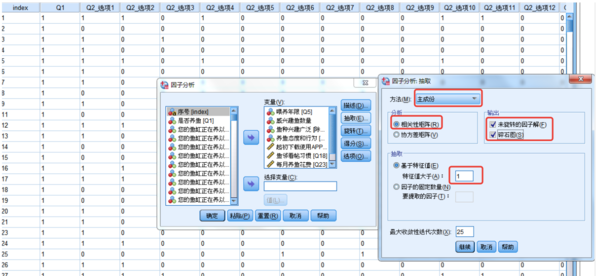
主成分分析法原理

　　主成分分析法是一种基于特征值分解和线性代数的统计技术。其目标是找到数据中的主要变换方向，这些方向被称为“主成分”，它们是线性无关的，并且按照方差的大小排序。通过将数据投影到这些主成分上，我们可以降低数据的维度，同时保留尽可能多的信息。

轻量版8.53的特点

　　与传统的主成分分析法相比，轻量版8.53具有以下特点： 1. 高效：计算速度快，适合处理大规模数据集。 2. 简单：使用更少的参数和算法步骤，易于理解和实施。 3. 灵活：可以根据不同的数据特性和需求进行调整。 4. 可扩展：可以轻松地与其他数据预处理和分析技术集成。 5. 免费：提供开源和免费的代码库，方便研究人员和实践者使用。

PCA轻量版8.53步骤

　　以下是使用轻量版8.53的主成分分析法进行数据降维的步骤： 1. 数据预处理：对数据进行中心化（减去均值）和标准化（除以标准差）。 2. 计算协方差矩阵：计算数据的协方差矩阵，以衡量数据特征之间的相关性。 3. 特征值分解：对协方差矩阵进行特征值分解，得到特征值和特征向量。 4. 选择主成分：根据特征值的大小选择前K个主成分，这些主成分可以解释大部分数据的方差。 5. 数据投影：将原始数据投影到选定的K个主成分上，得到降维后的数据。 6. 重构数据（可选）：如果需要，可以使用主成分将降维后的数据恢复为原始维度的数据。

应用案例

　　以下是轻量版8.53的主成分分析法在不同领域的应用案例： 1. 金融领域：用于股票价格的预测和风险评估，通过降维可以发现影响股票价格的潜在因素。 2. 生物信息学：用于蛋白质结构分析和功能预测，通过降维可以揭示蛋白质之间的相似性和差异。 3. 图像处理：用于图像压缩和人脸识别，通过降维可以提取图像的关键特征。 4. 语音识别：用于提取语音信号的特征，通过降维可以提供更高的识别准确率。 5. 推荐系统：用于提取用户兴趣和产品特征，通过降维可以提供更准确的推荐结果。

结论

　　主成分分析法是一种强大的数据降维技术，而轻量版8.53提供了更高效、简单的方法来应用这一技术。通过遵循上述步骤和应用案例，研究人员和实践者可以更好地理解和应用轻量版8.53的主成分分析法，从而在各自的领域中实现更好的数据理解和分析结果。

参考文献

　　[1] Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.

　　[2] Jolliffe, I. T. (2002). Principal Component Analysis (2nd ed.). Springer.

　　[3] Abdi, H., & Williams, L. J. (2010). Principal Component Analysis. WIREs Computational Statistics, 2(4), 433-459.